在几何学领域，中点弦专题是一个重要的知识点，涉及中点的性质、弦的性质以及它们在图形中的应用，本文将深入探讨中点弦专题的各个方面，帮助读者更好地理解这一几何概念的内涵和外延。

中点的性质

在几何学中，中点是线段上距离两个端点距离相等的点，中点具有许多重要的性质，例如线段的中点将该线段分为两个相等的部分，中点在三角形中具有独特的地位，与三角形的重心、垂心等存在密切关系。

弦的性质

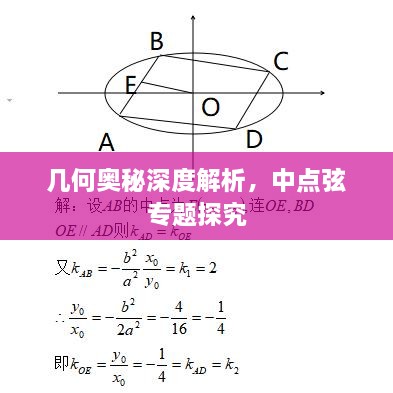
弦是几何图形中连接两个点的直线段，在圆中，弦与半径之间的关系是圆的重要性质之一，弦的中点也是研究弦性质的关键点之一，弦的中点到圆心的距离等于该弦的一半，弦与角的性质也有密切关系，如弦对应的圆周角相等时，弦也相等。

中点弦专题的应用

中点弦专题在几何学中有着广泛的应用，在解决与三角形有关的问题时，利用中点性质可以简化问题并找到解决方案，在解决与圆有关的问题时，利用弦的性质和中点弦专题的知识可以更加高效地找到答案，在解决与圆的切线有关的问题时，可以通过找到切线上某一点的中点，利用弦的性质来求解。

中点弦专题的深入解析

对于中点弦专题的深入解析，我们需要从多个角度进行探究，从代数几何的角度，我们可以探讨中点和弦的向量表示以及它们在平面上的运算，从解析几何的角度，我们可以分析如何通过坐标变换来求解中点弦问题，我们还可以从组合几何的角度来研究中点弦专题，探讨其与图形分割、面积计算等问题的联系。

实例分析

为了更好地理解中点弦专题，我们可以通过实例分析来加深认识，在解决三角形中的中线问题时，可以利用中点的性质将问题转化为更容易求解的形式，在解决与圆有关的问题时，可以通过找到弦的中点，利用弦的性质来求解，我们还可以通过分析一些经典的中点弦问题，如蝴蝶定理等，来深入理解这一专题的应用。

中点弦专题是几何学中的重要知识点，涉及中点的性质、弦的性质以及它们在图形中的应用，通过深入了解中点弦专题的各个方面，我们可以更好地应用这些知识来解决与三角形和圆有关的问题，为了更好地理解这一专题，我们需要从多个角度进行探究，并结合实例分析来加深认识，希望本文能帮助读者更好地理解中点弦专题的内涵和外延。